Holding Data to a Higher Standard, Part I: A Guide to Standard Production, Use, and Data Validation
Testing, manufacturing, and research laboratories face more challenges and regulations than ever before. Many accreditation bodies issue increasing numbers of guidelines. Regulatory agencies increase the number of compounds and elements that need to be reported while the levels of detection required are being decreased. There is often a lot of time, effort, and money invested in deciphering the data and determining its validity and accuracy. Here, we explore the accreditation, regulation, and guidelines around the manufacture and use of standards and certified reference materials (CRMs) and discuss the variables from accreditation to uncertainty involved in producing and using standards and reference materials. We also discuss the changing field of chemical analysis and the challenges that arise from the pursuit of increasingly smaller levels of detection and quantitation, including clean laboratory techniques to reduce analytical error and contamination in standards use and data collection.
The complex question of whether or not data or results are valid involves both the testing process and the actual calculated results. The question of whether or not the results reflect the true answer becomes a function of the accuracy of your standards.
Standards in the laboratory industry can be either procedural standards or metrological standards. A procedural or method standard is an authoritative quality system, procedure, or methodology considered by general consensus as the approved model or method. These types of standards are created by organizations such as the International Organization for Standardization (ISO), Association of Official Agricultural Chemists (AOAC), and American Section of the International Association for Testing Materials (ASTM), to name just a few. In some instances, laboratories seek accreditation to validate their procedures and methods to ensure some benchmark of accuracy and quality.
The second important type of standard used to determine data validity are metrological standards. A metrological standard is the fundamental example or reference for a unit of measure. Simply stated, a standard is the “known” to which an “unknown” can be measured. Metrological standards fall into different hierarchical levels. The highest levels of metrological standards are primary standards. A primary standard is the definitive example of its measurement unit to which all other standards are compared and whose property value is accepted without reference to other standards of the same property or quantity (1,2). Primary standards of measure, such as weight, are created and maintained by metrological agencies and bureaus around the world.
Secondary standards are the next level down within the hierarchy of standards. Secondary standards are close representations of primary standards that are measured against primary standards. Chemical standards companies often create secondary standards by comparing their material to a primary standard, making that standard traceable to a primary standard source. The third level of standards are working standards, which are often used to calibrate equipment and are created by comparison to a secondary standard.
There are also many standards designated as reference materials, reference standards, or certified reference materials. These materials are manufactured or characterized for a set of properties and are traceable to a primary or secondary standard. If the material is a certified reference material (CRM), then it must be accompanied by a certificate that includes information on the material’s stability, homogeneity, traceability, and uncertainty (2,3).
Stability, Homogeneity, Traceability, and Uncertainty
Stability is when a chemical substance is nonreactive in its environment during normal use. A stable material or standard will retain its chemical properties within the designated “shelf life” or within its expiration date if it is maintained under the expected and outlined stability conditions. A material is considered to be unstable if it can decompose, volatilize (burn or explode), or oxidize (corrode) under normal stated conditions.
Homogeneity is the state of being of uniform composition or character. Reference materials can have two types of homogeneity: within-unit homogeneity or between-unit (or lot) homogeneity. Within-unit homogeneity means there is no precipitation or stratification of the material that cannot be rectified by following instructions for use. Some reference materials can settle out of solution, but are still considered homogeneous if they can be redissolved into the solution by following the instructions for use (that is, sonicate, heat, shake). Between-unit or lot homogeneity is found between separate packaging units.
Traceability is the ability to trace a product or service from the point of origin through the manufacturing or service process through to final analysis, delivery, and receipt. Reference materials producers must ensure that the material can be traced back to a primary or secondary standard.
Uncertainty is the estimate attached to a certified value that characterizes the range of values where the “true value” lies within a stated confidence level. Uncertainty can encompass random effects such as changes in temperature, humidity, drift accounted for by corrections, and variability in performance of an instrument or analyst. Uncertainty also includes the contributions from within-unit and between-unit homogeneity, changes because of storage and transportation conditions, and any uncertainties arising from the manufacture or testing of the reference material.
Types of Uncertainty
There are two basic classifications for types of uncertainty: Type A and Type B uncertainty. Type A uncertainty is associated with repeated measurements and the statistical analysis of the series of observations. Type A uncertainty is calculated from the measurement’s standard deviation divided by the square root of the number of replicates.
Figure 1: Representations of accuracy and precision.
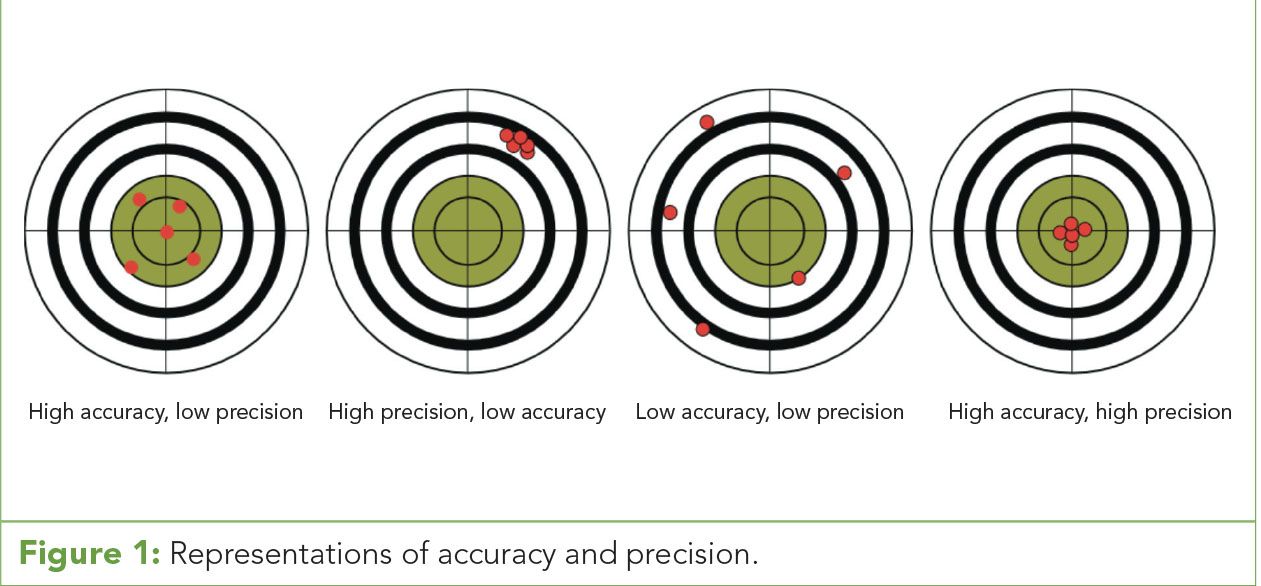
Table I: Accuracy and precision for absolute and relative errors

Type B uncertainty is based on scientific judgement made from previous experience and manufacturer’s specifications. Type B normal distribution is used when an estimate is made from repeated observations of a randomly varying process and an uncertainty is associated with a certain confidence interval. This type of uncertainty distribution is often found in a calibration certificate with a stated confidence level. Reference materials providers accredited by ISO 17025 and ISO 17034 provide certificates using combined and expanded uncertainties within a normal distribution. These certificates contain stated values and the uncertainty associated with that value as well as the contributions to those uncertainties.
True Value, Accuracy, and Precision
Uncertainty is not error or mistakes. Error causes values to differ when a measurement is repeated and is the difference between the stated measurement and the true value of the measurand. True values are never absolute. The nature of a true value is that it contains uncertainty and error, which make it somewhat indeterminate. True values are obtained by perfect and error-free measurements, which do not exist in reality. Instead, the expected, specified, or theoretical value becomes the accepted true value. Analysts then compare the observed or measured values against that accepted true value to determine accuracy or “trueness” of the data set.
Often, accuracy and precision are used interchangeably when discussing data quality. In reality, they are very different assessments of data and the acquisition process. Accuracy is the measurement of individual or groups of data points in relationship to the “true” value. In essence, accuracy is how close your data gets to the target and is often expressed as either a numerical or percentile difference between the observed result and the target or “true” value.
Precision, on the other hand, is the measurement of how closely the data points within a data set relate to each other. It is the measure of how well data points cluster within the target range and is often expressed as a standard deviation. Precision is an important tool for the evaluation of instrumentation and methodologies by determining how data is produced after varied replications (Figure 1). (See upper right for Figure 1, click to enlarge; Figure 1: Representations of accuracy and precision.)
Repeatability and reproducibility measure the quality of the data, method, or instrumentation by examining the precision under the same (minimal difference) or different (maximal difference) test conditions. Repeatability (or test–retest reliability) is the measurement of variation arising when all the measurement conditions are kept constant. These conditions typically include location, procedure, operator, and instrument run in repetition over a short period of time.
Reproducibility is the measurement of variation arising in the same measurement process occurring across different conditions such as location, operator, instruments, and over long periods of time.
Estimating Error
Another way of looking at accuracy and precision is in terms of measuring the different types of error. If accuracy is the measurement of the difference between a result and a “true” value, then error is the actual difference or the cause of the difference. The estimation of error can be calculated in two ways, either as an absolute or relative error. Absolute errors are expressed in the same units as the data set and relative errors are expressed as ratios, such as percent or fractions.
Absolute accuracy error is the true value subtracted from an observed value and is expressed in the same units as the data. Errors in precision data are most commonly calculated as some variation of the standard deviation of the data set. An absolute precision error calculation is based on either the standard deviation of a data set or values taken from a plotted curve. A relative precision error is most commonly expressed as relative standard deviation (RSD) or coefficient of variance (CV or %RSD) of the data set (Table I). (See upper right for Table I, click to enlarge; Table I: Accuracy and precision for absolute and relative errors.)
The most common error in regards to data are observational or measurement errors, which are the difference between a measured value and its true value. Most measured values contain an inherent aspect of variability as part of the measurement process, which can be classified as either random or systematic errors.
Random (or indeterminate) errors lead to measured values that are inconsistent with repeated measurements. Systematic (or determinate) errors are introduced inaccuracy from the measurement process or analytical system. There are some basic sources for systematic error in data such as operator or analyst, apparatus and environment, and method or procedure. Systematic errors can often be reduced or eliminated by observation, record-keeping, training, and maintenance.
Understanding and Compensating for Indeterminate Error
Random or indeterminate errors arise from random fluctuations and variances in the measured quantities and occur even in tightly controlled analysis systems or conditions. It is not possible to eliminate all sources of random error from a method or system. However, random errors can be minimized by experimental or method design. For instance, while it is impossible to keep an absolute temperature in a laboratory at all times, it is possible to limit the range of temperature changes. In instrumentation, small changes to the electrical systems from fluctuations in current, voltage, and resistance cause small continuing variations that can be seen as instrumental noise. The measurement of these random errors is often determined by the examination of the precision of the generated data set. Precision is a measure of statistical variability in the description of random errors. Precision analyzes the data set for the relationship and distance between each of the data points independent of the “true” or estimated value of the data to identify and quantify the variability of the data.
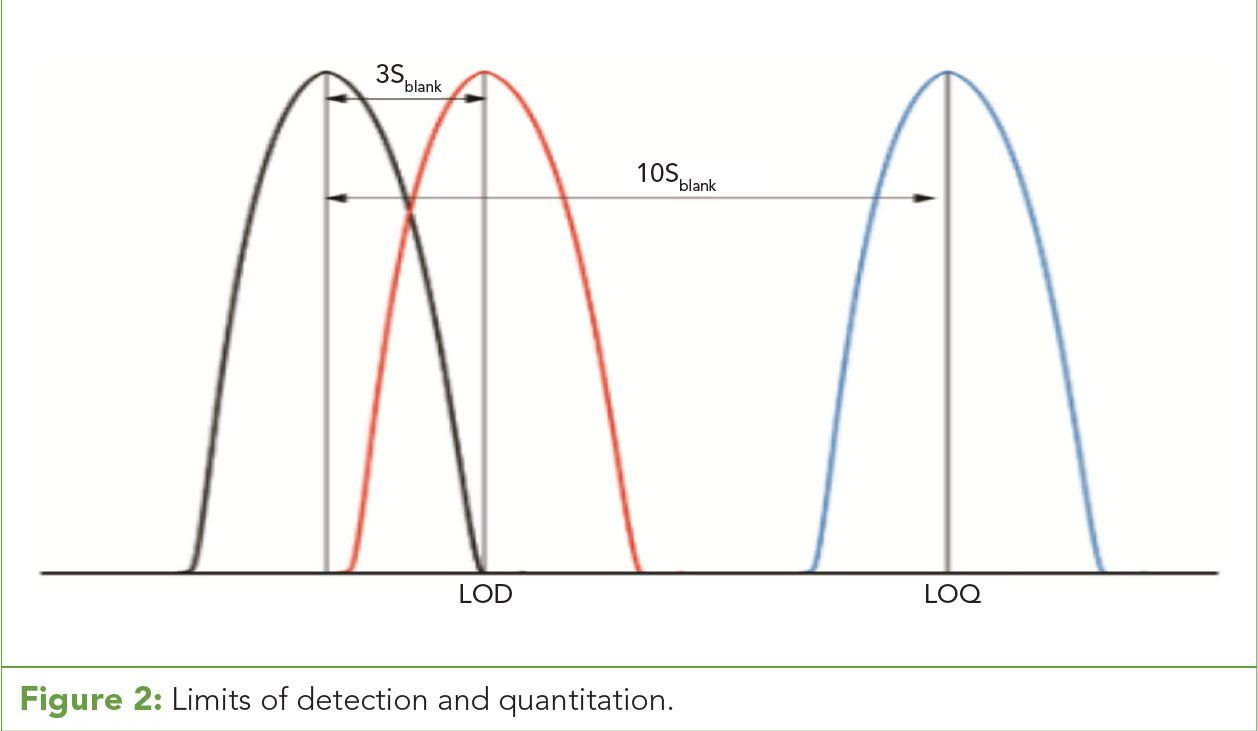
Figure 2: Limits of detection and quantitation.
Accuracy is the description of systematic errors and is a measure of statistical bias that causes a difference between a result and the “true” value (trueness). A second definition, recognized by ISO, defines accuracy as a combination of random and systematic error that then requires high accuracy to also have high precision and high “trueness.” An ideal measurement method, procedure, experiment, or instrument is both accurate and precise with measurements that are all close to and clustered around the target or “true” value. The accuracy and precision of a measurement value is a process validated by the repeated measurements of a traceable reference standard or reference material.
Using Standards and Reference Materials
Certified standards or CRMs are materials produced by standards providers that have one or more certified values with uncertainty established using validated methods and are accompanied by a certificate. The uncertainty characterizes the range of the dispersion of values that occurs through the determinate variation of all the components that are part of the process for creating the standard.
Each of the components in the creation of the standard have a calculated uncertainty, which then are all combined to create a combined uncertainty associated with the certified value. For example, in the creation of a chemical standard there could be separate uncertainties for all the volumetric glassware used in the production of the standard as well as uncertainty from the purity of the starting material, variations in the balance, temperature of the laboratory, and purity of the solvents. Each uncertainty for individual components is calculated and added together to form the combined uncertainty for the standard. To be clear, the uncertainty listed on a standard certificate is the measured uncertainty for that standard’s certified value and not the expected range of results for an instrument or test method. Each test method or instrument carries its own set of uncertainty calculations that determine the accuracy and precision of that analytical method, which is independent of the value on the certificate of the standard.
CRMs have a number of uses, including validation of methods, standardization or calibration of instruments or materials, and quality control and assurance procedures. A calibration procedure establishes the relationship between a concentration of an analyte and the instrumental or procedural response to that analyte. A calibration curve is the plotting of multiple points within a dynamic range to establish the analyte response within a system during the collection of data points. One element of the correct interpretation of data from instrumental systems is the effect of a sample matrix on an instrumental analytical response. The matrix effect can be responsible for either analyte suppression or enhancement. In an analysis where matrix can influence the response of an analyte, it is common to match the matrix of analytical standards or reference materials to the matrix of the target sample to compensate for matrix effects.
Different approaches to using calibration standards may need to be employed to compensate for the possible variability within a procedure or analytical system. Internal standards are reference standards that are either similar in character or analogs of the target analytes that have a similar analytical response are added to the sample before analysis. In some cases, deuterated forms of the target analytes are used as internal standards. This type of standard allows the variation of instrument response to be compensated for by the use of a relative response ratio established between the internal standard and the target analyte. A second type of internal standard is a standard addition or spiking standard. In some analyses, the matrix response, instrument response, and analyte response are indistinguishable from each other because the analyte concentration nears the lower limit of detection or quantitation. A target standard can then be added in known concentration to compensate for the matrix or instrument effects to bring the signal of the target analyte into a quantitative range.
External standards are multiple calibration points that contain standards or known concentrations of the target analytes and matrix components. Depending on the type of analytical techniques, linear calibration curves can be generated between response and concentration that can be calculated for the degree of linearity or the correlation coefficient (r). An r value approaching 1 reflects a higher degree of linearity, most analysts accept values of >0.999 as acceptable correlation.
Calibration curves are often affected by the limitations of the instrumentation. Data can become biased by calibration points influenced by instrument limits of detection, quantitation, and linearity. Limit of detection (LOD) is the lower limit of a method or system at which the target can be detected as different from a blank with a high confidence level (usually over three standard deviations from the blank response). The limit of quantitation (LOQ) is the lower limit of a method or system at which the target can be reasonably calculated where two distinct values between the target and blank can be observed (usually over 10 standard deviations from the blank response) (4) (Figure 2). (See upper right for Figure 2, click to enlarge; Figure 2: Limits of detection and quantitation.)
Figure 3: Calibration curve limits and range.

A second method of determining levels of detection and quantitation can be considered using the signal-to-noise ratio (S/N). The signal-to-noise ratio is the response of an analyte measure on an instrument as a ratio of that response to the baseline variation (noise) of the system. Limits of detection are often recognized as target responses that have three times the response of baseline noise or S/N ≥ 3. Limits of quantitation are recognized as target responses which have 10 times the response of baseline noise or S/N ≥ 10.
Limits of linearity (LOL) are the upper limits of a system or calibration curve where the linearity of the calibration curve starts to be skewed creating a loss of linearity (Figure 3). (See upper right for Figure 3, click to enlarge; Figure 3: Calibration curve limits and range.) This loss of linearity can be a sign that the instrumental detection source is approaching saturation. The array of data values between the LOQ and the LOL is considered to be the dynamic range of the system where the greatest potential for accurate measurements will occur.
The understanding of a system’s dynamic range and the accurate bracketing of calibration curves within the range and around the target analyte concentration increase the accuracy of the measurements. If a calibration curve is created that does not potentially bracket all the possible target data points, then the calibration curve can be biased to artificially increase or decrease the results and create error.
Conclusion
The elimination of error from analytical methods is an ongoing process that forces the analytical laboratory to examine all their processes to eliminate sources of systematic error and mistakes. It is then a process of identifying the sources of random error in the analysis and sample preparation procedures to calculate the uncertainty associated with each source. Standards and certified reference materials give an analyst the known quantity, character, or identity to reference against their samples and instruments to further eliminate error and increase accuracy and precision to bring them closer to their goal of determining the true value.
References:
- âInternational Vocabulary of Metrology – Basic and General Concepts and Associated Terms (VIM), 3rd Edition (JCGM member organizations [BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML] 200, 2012). Available at: http://www.bipm.org/vim.
- International Organization for Standardization (ISO) Guide 30, "Terms and Definitions Used in Connection with Reference Materials."
- International Organization for Standardization (ISO) ISO Guide 17034, "General Requirements for the Competence of Reference Material Producers."
- Standard Format and Guidance for AOAC Standard Method Performance Requirement (SMPR) Documents (Version 12.1; 31-Jan-11).
Patricia Atkins is a Senior Applications Scientist with SPEX CertiPrep in Metuchen, New Jersey. Direct correspondence to: patkins@spex.com
How to Cite This Article
P. Atkins, Cannabis Science and Technology1(2), 44-48 (2018).

The Cost of Compliance in the Cannabis Industry
April 1st 2025The financial and reputational risks of non-compliance far outweigh the upfront investment required to establish robust compliance systems. This blog explores the true cost of compliance, what non-compliance can mean for a business, and why investing in compliance is a proactive, strategic decision rather than a burdensome expense.