Calibration Science, Part IV: Calibration Metrics
Here, we discuss the importance of calibration metrics and how to measure calibration quality.
Now that we have discussed calibration lines, we now need to discuss how to measure their quality, that is, we need to study calibration metrics. We will discuss variance and how it is measured. Then, using illustrations and equations we will see how to calculate the standard deviation of a data set, which will give us a measure of accuracy; how to calculate the correlation coefficient, which was introduced in the last column; and the F for Regression, a measure of a thing called the robustness of a calibration, which is an obscure but important measure of calibration quality.
Variance
Hold on to your hats. To understand calibration metrics, we must talk about statistics. I will try to make this as painless as possible, using words and figures in addition to equations to explain things.
The mathematical concept of variance is also known as scatter or dispersion. In a set of data, variance is a measure of how the data are distributed with respect to the average of data. This is illustrated in Figure 1.
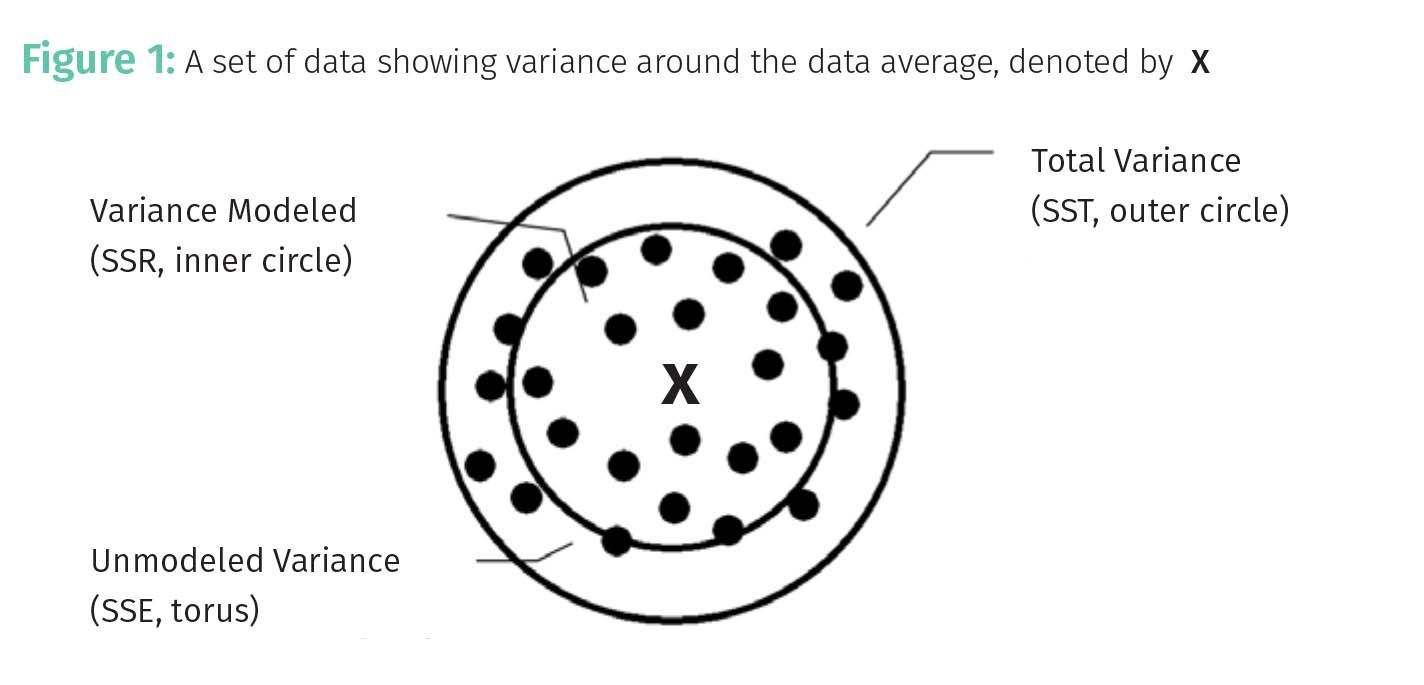
In Figure 1, the black dots represent data points, and the X represents the average of the data set. To put this all in concrete terms I will use the isopropanol (IPA) in water infrared spectroscopy calibration line example from last time (1). The peaks used in the peak area calculations are shown in Figure 2, the standard concentration and peak area data are in Table 1, and the actual calibration line is in Figure 3.
Note in Table 1 that the %IPA concentrations vary from 9% to 70%, this is an example of variance. The average of the %IPA values in Table 1 is 37%, this would be the X at the center of Figure 1. This variation in IPA concentrations listed in Table 1 is intentional: we varied the standard concentrations to obtain a concentration range that brackets those of the expected unknowns, a principle discussed before (2). Unintentional variance comes from random and systematic error, which we have also discussed (3). Imagine the data points in Figure 1 are the predicted values obtained by applying the calibration seen in Figure 3 to the spectra in Figure 2. Thus, in our example the total variance is equal to the sum of the variance from using standards with different concentrations AND from the error. Both these sources contribute to the variance seen in Figure 1. How do we go about quantifying this variance? Well, keep reading.
Variance in Pictures and Equations
Note that the outer circle in Figure 1 is labeled “total variance” and is obtained by simply drawing a circle that includes all the data points as shown. To measure the distance, that is, variance from any given data point i to the average, we can simply subtract their values as seen in Equation 1:
where Vi is the variance of data point I; Yi is the value of data point I; and Y is the average of all data points.
Remembering that in our example each Yi is simply a predicted %IPA value.
The total variance then would be the sum of all variances for all the data points as given by Equation 2:
where Σi is the sum over all variances; Yi is the value of data point I; and Y is the average of all data points.
Now the tricky bit here is some of the variances will have positive values, and some negative values, and when the sum is calculated they will cancel, not giving the true size of the variance. That is why rather than using Equation 2 to measure the total variance, we square each individual variance so all the values are positive, then add these numbers together as seen in Equation 3:
where SST is the sum of squares total, the total variance; Σi is the sum over all variances; Yi is the actual value of data point I; and Y is the average of all data points.
Now given the outer circle seen in Figure 1 spans the total variance, the SST is the calculated total variance, is the area of this circle. Hence in Figure 1 it says “SST, Total Variance, Outer Circle”.
Now, no model will predict all standard concentrations with 100% accuracy because of random and systematic error. In other words, for the calibration line seen in Figure 3 the line will never pass through the center of all the data points, although this calibration line is close to that ideal. This means calibration models can model some variance but not all of it. How then do we measure the variance accounted for by a model? That would be seen in Equation 4:
where SSR is the sum of squares explained by regression (the variance modeled); Y’ is the predicted value; and Y is the average value.
The term SSR is annoying, but is what is used in the literature. It is simply the variance accounted for by a model, but the “regression” thing is assuming we are using a regression algorithm, which in this case we are: linear regression.
In our example, each Y’ would be a predicted %IPA value as determined by applying the equation for the calibration line seen in Figure 3 to the peak area data seen in Table 1. Each (Y’ – Y) is the difference between each predicted value and the average, then everything is squared to get all positive numbers, and all this is added together. In terms of the diagram in Figure 1, the SSR is the area of the inner circle, hence it says, “Variance Modeled, SSR, Inner circle.” This makes sense because the SSR is based on the difference between the predicted values, the variance accounted for by the model, and the average.
What we have left to calculate is the variance not accounted for by the model. In other words, the magnitude of the total error in the model predictions. For the calibration line in Figure 3 this would be the space between the known %IPA standard values and the average. How do we calculate this? Equation 5, of course:
where SSE is the sum of squares due to error (variance not modeled); Yi is the actual value; and Y’ is the predicted value.
The SSE, the sum of squares due to error, quantifies the variance not modeled, and is the sum of the squares of the difference between the predicted and actual values. For our IPA example, Yi would be the known IPA%, and Y’ would be the predicted % IPA for each sample. The SSE corresponds to the area of the torus in Figure 1, where it says “Unmodeled variance, SSE, torus”.
Equations 3-5 are known as the “sums of squares” equations because in each case a quantity is calculated, it is squared, and then summed. To summarize, the SST is the sum of squares total, measures the total variance, and depends upon the actual values and their average. The SSR is the sum of squares accounted for by regression, measures the amount of variance accounted for by a calibration model, and depends upon the predicted values and the average. Lastly, the SSE is the sum of squares due to error, and depends on the actual and predicted values.
Calibration Metrics
Standard Deviation
Now we come to the reason why we slogged through all the math and statistics above, to be able to derive equations that tell us the quality of calibrations obtained with analytical instruments. The standard deviation, σ, is something we have discussed in the past (4). My way of explaining is that it is the average error per data point in a data set. In our %IPA example it would be the average error between the known and predicted %IPA values. If you look at the SSE equation (Equation 5) above, note that it also depends upon the known values, Yi, and the predicted values Y’. So, can we use SSE to calculate the standard deviation? Yes, we can as given by Equation 6:
where σ is the standard deviation; SSE is the sum of squares due to error; and n is the number of data points.
If our data points are in units of %IPA, the SSE is in units of (%IPA)2, hence the need to take the square root of the term on the right-hand side in Equation 6. The number of data points, n, in terms of analytical instrument calibrations, is the number of standards used. For our IPA example, it is 5 as taken from the data in Table 1. Equation 6 is consistent with other equations I have presented to calculate the standard deviation as it has the total error in the numerator and the number of samples in the denominator.
Correlation Coefficient
The correlation coefficient, R, was mentioned in the last column (1). If you look closely at Figure 1 the big circle represents SST, the inner circle SSR, and the torus SSE. Visually, you can see that the area of the big circle is equal to the area of the inner circle and the torus. In other words, the total variance equals the sum of the variance modeled and the variance not modeled (due to error) as expressed in Equation 7:
where SST is the sum of squares total, the total variance; SSR is the sum of squares due to regression, the variance modeled; and SSE is the sum of squares due to error, the variance not modeled.
Recall (1) that the correlation coefficient is on a 0 to 1 scale, where 1 means a perfect correlation between actual and predicted values, and 0 means there is no correlation. Note that I said R depends upon actual and predicted values, well so does the SSE seen in Equation 5, thus we can write how R is calculated in Equation 8:
where R is the correlation coefficient; SSR is the sum of squares due to regression (variance modeled); and SST is the sum of squares total (total variance).
Note that in Equation 8, R is calculated as a ratio. What R really represents is the fraction of variance accounted for by a model. If SSR = SST there is no error, and we get R = 1. If none of the variance is modeled SSR = 0 and R = 0. Thus, we now know why R is on 0 to 1 scale.
A final calibration metric that is useful to calculate is the F for Regression (5). It is given by Equation 9:
where F is the F for regression; SSR is the sum of squares due to regression; SSE is the sum of squares due to error; n is the number of data points (number of samples); and m is the number of independent variables.
The first term in Equation 9, SSR/SSE, is the ratio of the variance modeled to the variance unmodeled, that is the error. This is a lot like a signal to noise ratio, which we have talked about before (3). The greater the variance modeled compared to the variance unmodeled, the better the model. The variable m is 1 for our %IPA example.
The F for regression is a measure of the robustness of a calibration, which is a measure of how strongly the model responds to changes in the input values. In the real world a robust stance is when you are standing on two feet, a small poke will not topple you over. A non-robust stance would be standing on one foot, and the same small poke may be enough to topple you over. Similarly, calibrations may be accurate but not robust because a small change in conditions can have a huge effect on the results. Therefore, robust calibrations are always preferred, sometimes even at the expense of accuracy.
Conclusions
Variance is a measure of the spread or scatter in the data, and for calibrations the total variance equals the variance modeled plus the variance unmodeled. The three sums of squares equations measure the total variance, SST, the variance modeled, SSR, and the error, SSE. The calibration metrics of the standard deviation, correlation coefficient, and F for regression can be calculated from these quantities.
References
- Smith, B., Calibration Science, Part III: Calibration Lines and Correlation Coefficients, Cannabis Science and Technology, 2024, 7 (2), 6-11.
- Smith, B., Quantitative Spectroscopy: Practicalities and Pitfalls, Part I, Cannabis Science and Technology, 2022, 5 (5), 8-13.
- Smith, B., Calibration Science, Part II: Systematic Error, Signal-to-Noise Ratios, and How to Reduce Random Error, Cannabis Science and Technology, 2024, 7 (1), 8-11.
- Smith, B., Statistics for Cannabis Analysis, Part I: Standard Deviation and Its Relationship to Accuracy and Precision, Cannabis Science and Technology, 2021, 4 (8), 8-13.
- Brian C. Smith, Quantitative Spectroscopy: Theory and Practice, 2002.
About the Columnist
Brian C. Smith, PhD, is Founder, CEO, and Chief Technical Officer of Big Sur Scientific. He is the inventor of the BSS series of patented mid-infrared based cannabis analyzers. Dr. Smith has done pioneering research and published numerous peer-reviewed papers on the application of mid-infrared spectroscopy to cannabis analysis, and sits on the editorial board of Cannabis Science and Technology. He has worked as a laboratory director for a cannabis extractor, as an analytical chemist for Waters Associates and PerkinElmer, and as an analytical instrument salesperson. He has more than 30 years of experience in chemical analysis and has written three books on the subject. Dr. Smith earned his PhD on physical chemistry from Dartmouth College. Direct correspondence to: brian@bigsurscientific.com
How to Cite this Article
Smith, B., Calibration Science, Part IV: Calibration Metrics, Cannabis Science and Technology, 2024, 7(3), 8-11.
